費用効果分析のためのモデル設計とシミュレーション
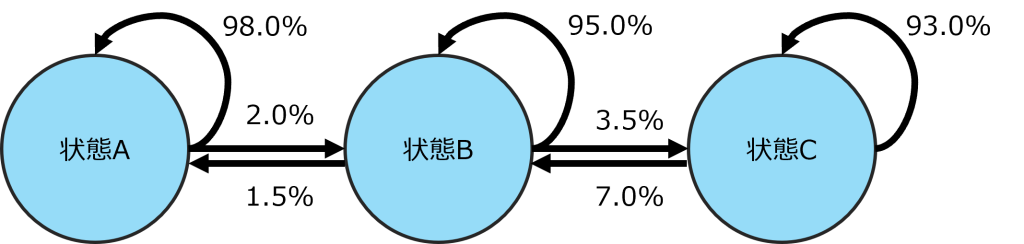
費用効果分析に用いられるモデルは、コホートレベルのモデルと患者レベルのモデルに分類されます1日本製薬工業協会 データサイエンス部会、 患者レベルのモデルを用いた費用効果分析、日本製薬工業協会ホームページ、2019年、https://www.jpma.or.jp/information/evaluation/results/allotment/lofurc000000a1xt-att/cost_effectiveness_modelling.pdf、2025年6月4日。コホートレベルのモデルは患者集団としてのアウトカムを求めるモデルで、決定木モデルやコホートベースのマルコフモデル(状態遷移モデル)、その混合モデルが使用されます。決定木モデルは、最初の健康状態[状態A]から次の健康状態(例えば改善状態[状態B]と非改善状態[状態C])へ確率的に移行するモデルです。長期的な時間推移を考慮しにくく、短期的なイベントを対象とした評価に使われることが一般的です。マルコフモデルはある健康状態と他の健康状態との間の遷移を遷移確率により定義し、一定単位の時間経過ごとに各健康状態(例えば、初期ステージ[状態A]、悪化ステージ[状態B]、最終ステージ[状態C])にある患者割合をシミュレーションするモデルです。いずれのモデルも、医療技術①と②の間の有効性の違いを、状態間を移行する確率の違いで表現します。最終的に、各健康状態にある患者割合に生じる差をもとに、費用と効果を算出します。

患者レベルのモデルの例としては離散イベントシミュレーション(DES:Discrete Event Simulation)があります。ひとりの患者において、連続的な時間の中で発生する離散的なイベントを十分に多くの患者でシミュレーションすることで、費用や効果の期待値を求めるモデルです。
各モデルの時間の取り扱い方としては、決定木モデルでは多くの場合時間を明示的に扱わないのに対して、マルコフモデルでは1か月おき、あるいは1年おきのように時間を離散的に扱い、DESでは連続的に扱う、という違いがあります。
そのほかの分析手法:費用最小化分析と費用便益分析
費用最小化分析は、費用対効果における「効果」の部分に有意な差がない(効果が同等である)ふたつの医療技術の費用を比較します。この分析では、費用が小さい医療技術の方が費用対効果に優れていると判断します。
費用便益分析は、費用対効果における「効果」の部分を金銭価値に変換して表し、その純便益(費用-便益)と費用便益比(費用/便益)で比較します。しかし、医療技術による「効果」を適切に「便益」に変換する手法が確立されていないため、広く使われていないのが現状です。
この記事はメール会員専用の記事です。
メール会員登録すると続きをお読みいただけます。